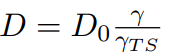1 固體中的傳輸
1.1 擴散Diffusion
化學反應的普通模型,可以被用來表示熱力學啟動擴散thermally activated diffusion.
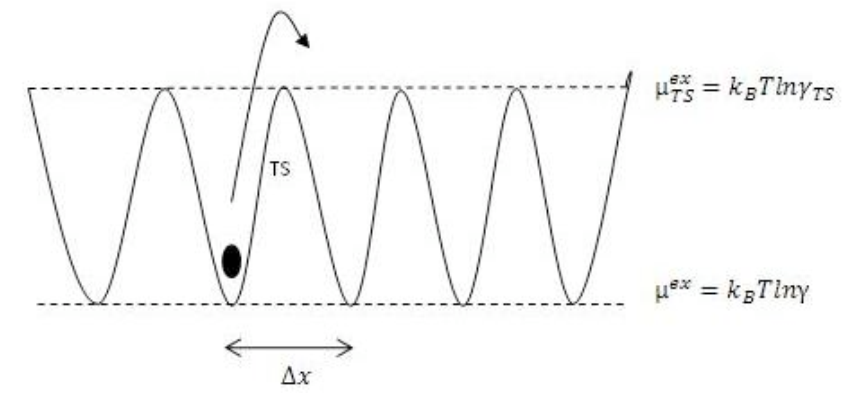
此過多的化學位能,就如同分子狀態的位能量。沒有飄移或偏壓的熱力學啟動轉移屬於隨機漫步,其中擴散係數是(轉移)步伐間中數平均時間mean-average time的函數:
擴散係數
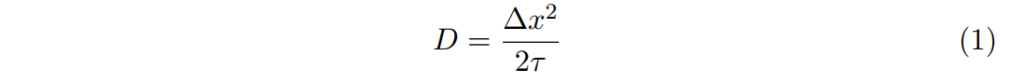
轉移中數平均時間也是轉移狀態transition state與穩定初始狀態stable original state間的位能差距potential energy gap函數。
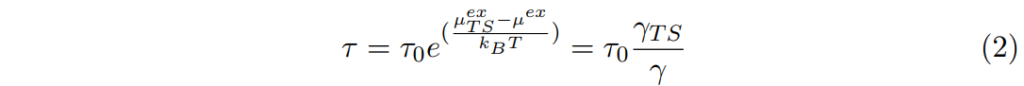
1/τ0∝T = 轉移的嘗試次數,同時回想 µex = kBT ln γ
最後,我們可以以啟動係數activity coefficients表示固體的擴散係數diffusivity:
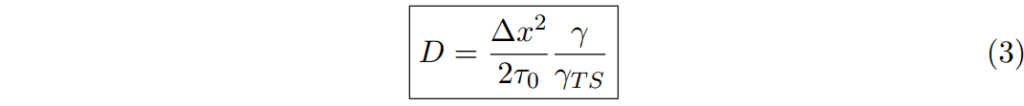
若繼續討論則可在某些特殊情況下,進一步簡化擴散係數表示式。
1.1.1 稀釋限制Dilute limit
一般接受的假設為γ及γTS並不受濃度 c 的影響。
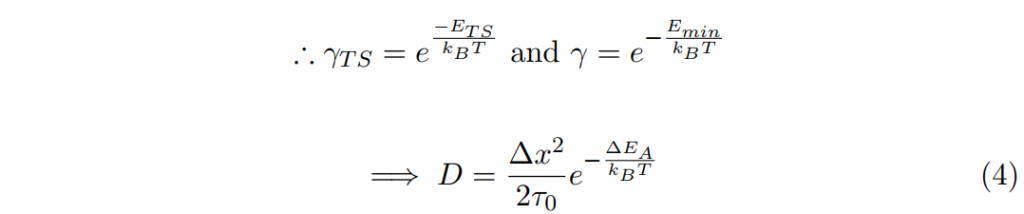
其中ΔEA = ETS – Emin為啟動能量障礙。
1.1.2 理想固體溶液(晶格氣體Lattice gas)
模型:
考慮一晶格氣體模型,其轉移狀態需要兩個空缺。因此我們有:
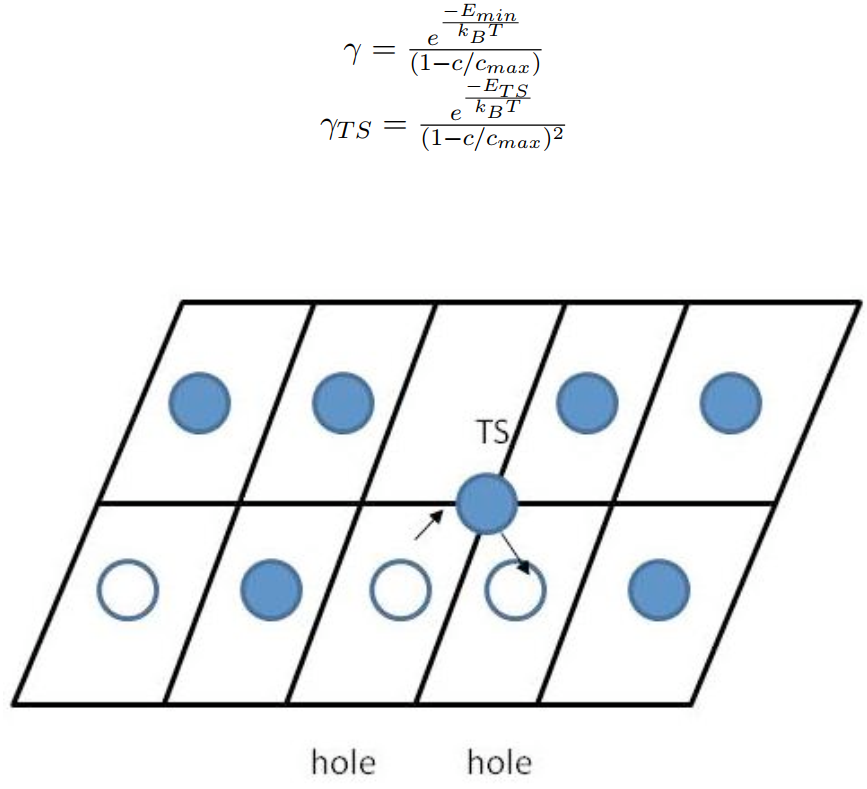
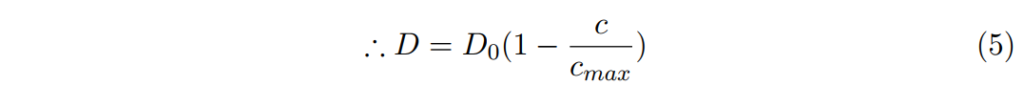
參數(1-c/cmax)可以被理解為假設分子由特定位置開始(狀態1),目標位置(狀態2)是空的機率。
1.1.3 一般性情況
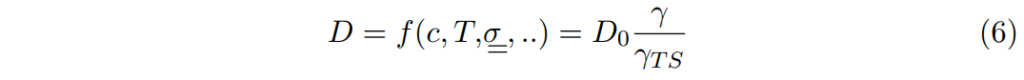
範例:![]() 為應力張量。
為應力張量。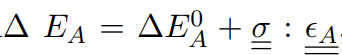 , 其中
, 其中![]() 為啟動應變張量,可以描述轉移狀態的形狀。
為啟動應變張量,可以描述轉移狀態的形狀。
→應力輔助的固體擴散stress-assisted diffusion in solids
1.2 飄移
我們現在只看當距離為 x 時的化學位能梯度函數:
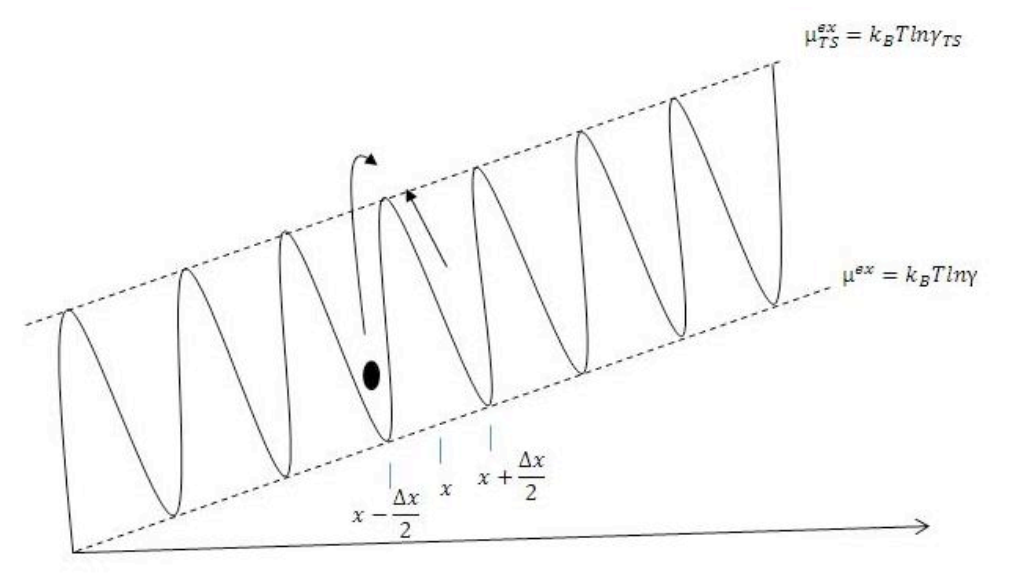
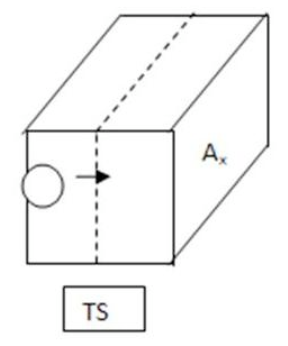
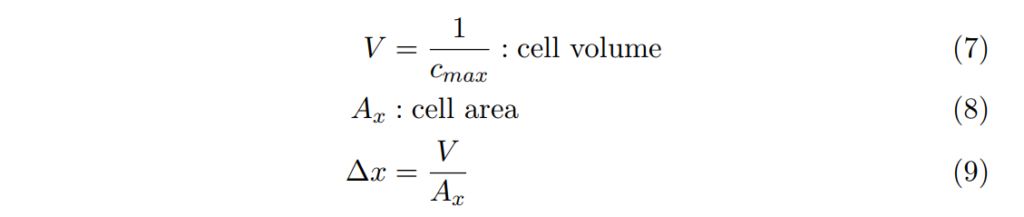
通量 F = R/Ax , 其中R為x方向上淨飄移的反應速率。
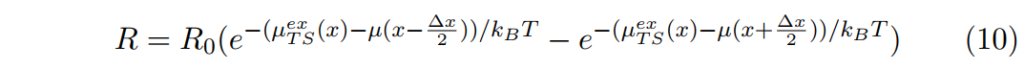
R0 = 1/2τ0 (因自障礙barrier完成轉移transition的機率為1/2)
假設 µ(x) 在分子尺度變化得極慢。
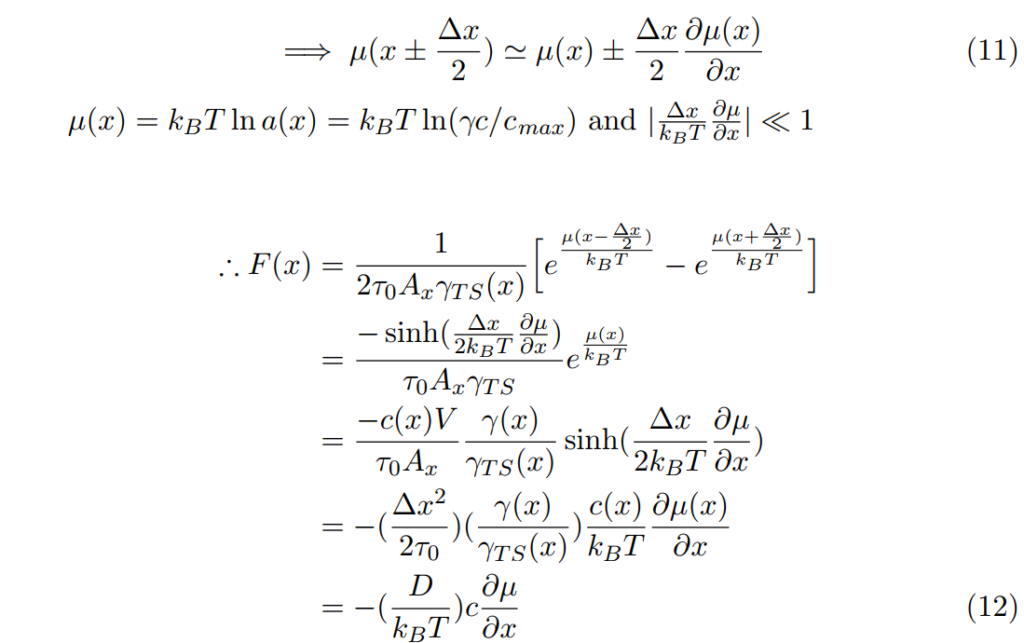
此處,![]() 一般性/熱力學力道。從未平衡熱力學nonequilibrium thermodynamics的基本假設可知:
一般性/熱力學力道。從未平衡熱力學nonequilibrium thermodynamics的基本假設可知:
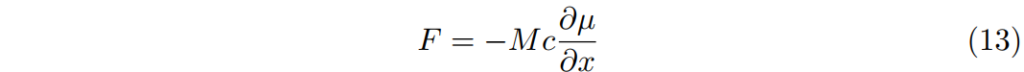
其中M是移動性mobility (速度/力量=1/拉力)
這正象徵著愛因斯關係:
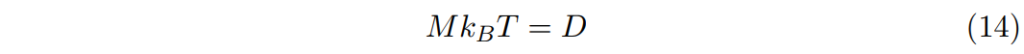
示蹤劑的移動性一般和他的擴散係數相關,即使是濃縮溶液(或固體)。
範例:固態溶液/晶格氣體
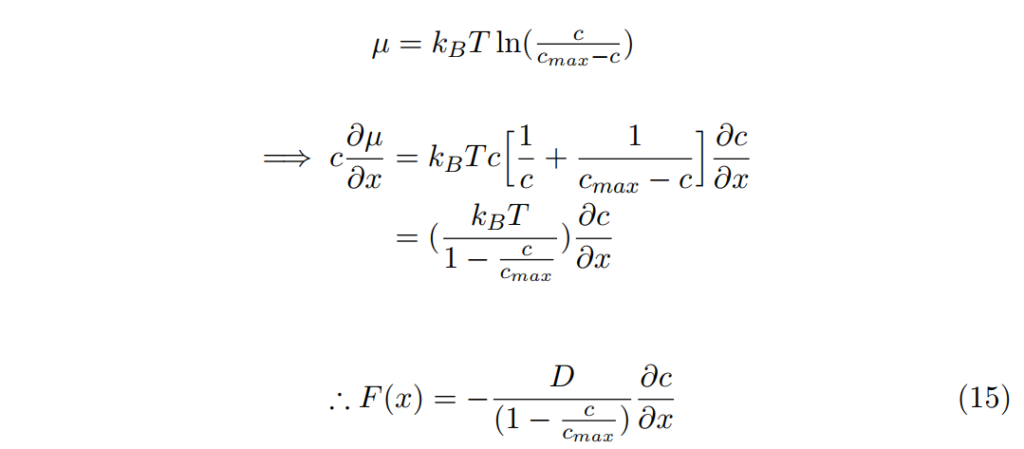
我們可以看到當c→cmax時因周邊範圍的強力作用使熱力學驅動力崩潰。然而,示蹤劑的擴散係數趨近於零在相同的限制下,因缺乏分子可以前往的空缺,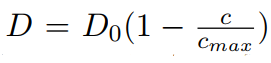 . 這會導致可觀的非線性反應取消現象,因化學擴散對不同濃度都是定值且等於分子或空缺示蹤劑的擴散係數。
. 這會導致可觀的非線性反應取消現象,因化學擴散對不同濃度都是定值且等於分子或空缺示蹤劑的擴散係數。
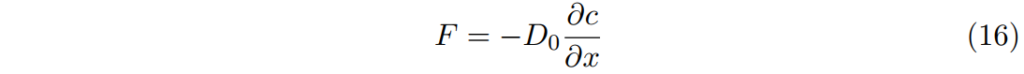
菲克定律 Fick’s law
在晶體中更一般性地說,若對晶格氣體假設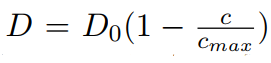 , 那對所有的μ(c, x, …)模型,
, 那對所有的μ(c, x, …)模型,
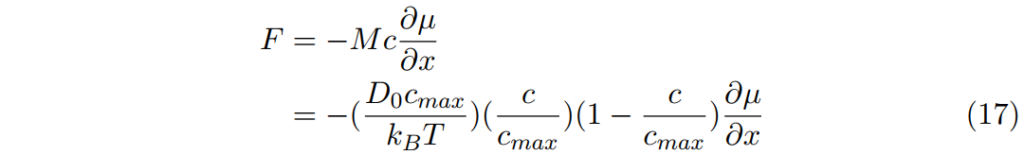
以此通量的守恆方程式為
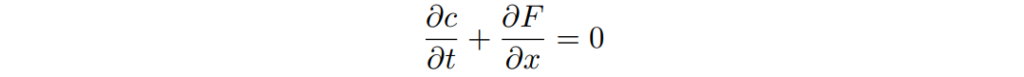
並在固態溶液或晶格氣體為Cahn-Hilliard方程式產生一適當的形式。(見課程38)
2 濃縮溶液理論
濃縮溶液化學位能為:
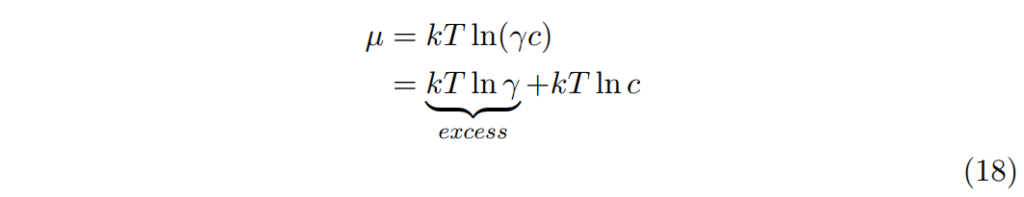
因此,濃縮溶液中的通量F為
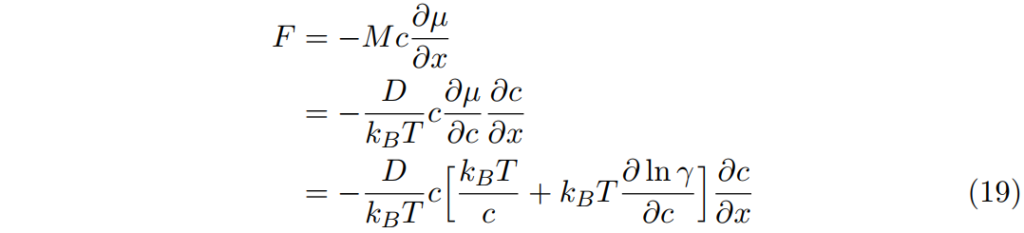
也常被改寫為
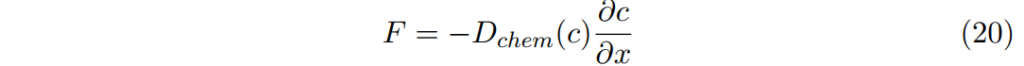
此處,Dchem有兩效果共同貢獻。

其中