電化學能量系統 課程3: 電化學能量儲存

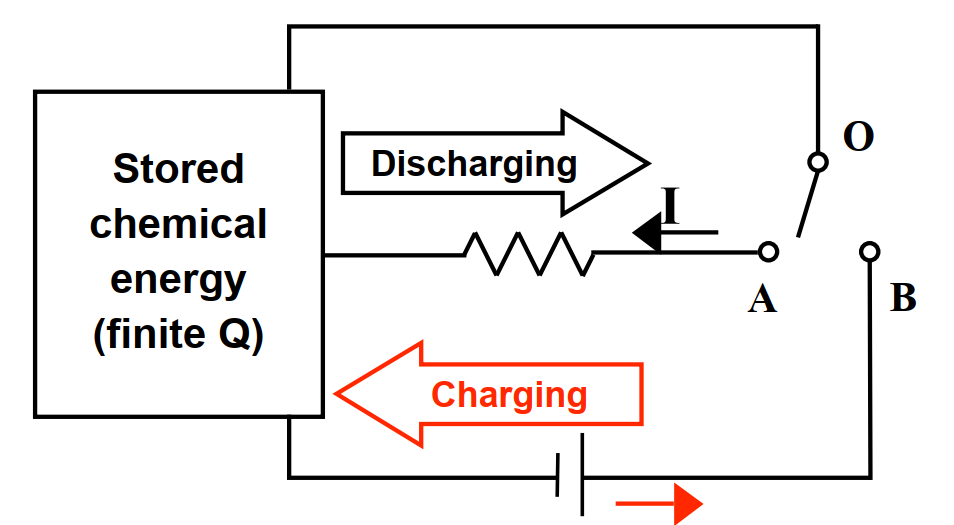
在這堂課，我們將學習電化學能量儲存數例。一般性電化學能量儲存概念如圖1。當一電化學能量系統連接外部源時(如圖1中的OB連接)，其就由外源充電並在充電期間儲存特定電荷Q. 系統在充電過程中將電能轉化為儲存的化學能。當系統連接到外部電阻電路(如圖1中的OA連接)時，他便釋放特定電荷Q並驅使流經外部電路的電流。系統在放電過程中將儲存的化學能轉換為電能。

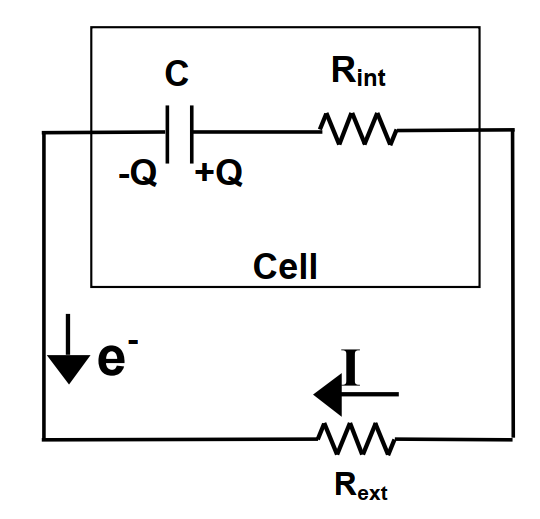
電容式能量儲存的簡單範例。圖2顯示了電容放電時的基礎電路。此處我們討論的是集成電容intergral capacitance. 電容值的大小是定義為一常數

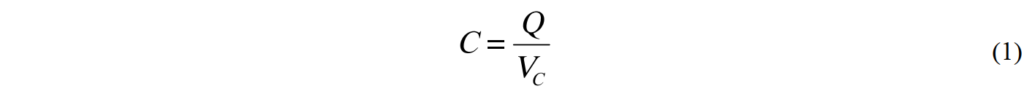
電流為

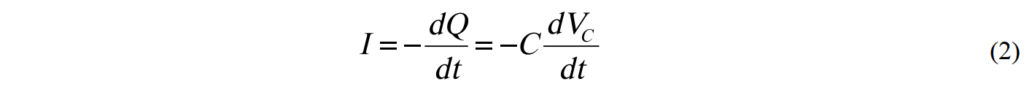
施加於外部電阻的電壓為

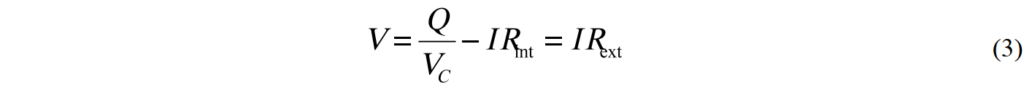
將(1)與(2)帶入(3)並使用總電阻R = R_int + R_ext, 則得到

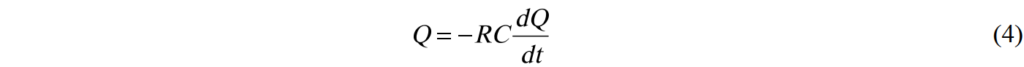
帶入初始狀態Q(t=0) = Q₀, 我們可以解方程式而得到

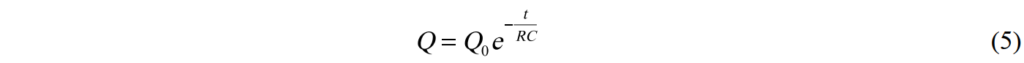
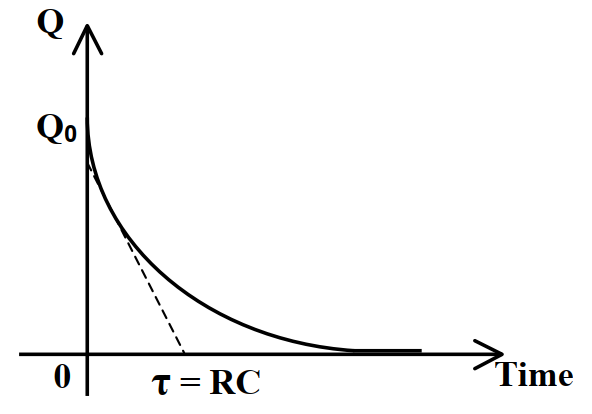
儲存的能量和時間關係如圖3，其中τ = RC稱為時間常數decay time.

在接下來的章節中，我們將介紹電化學能量儲存數個實際案例。

1. 超級電容

超級電容(supercapacitor or ultracapacitor)是一種電化學電容且較尋常電容有特別高的能量密度，通常比高電容的電解電容多上數千倍。一般來說，超級電容由奈米多孔性材料改善能量密度，如圖4。兩個多孔性電極被浸在同一電解液中，電荷則儲存在電化學雙層electrochemical double layers中。

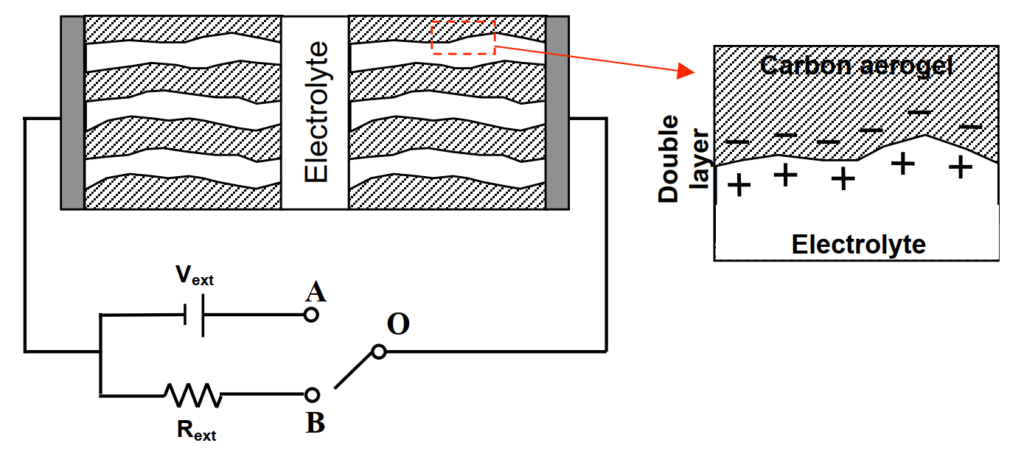
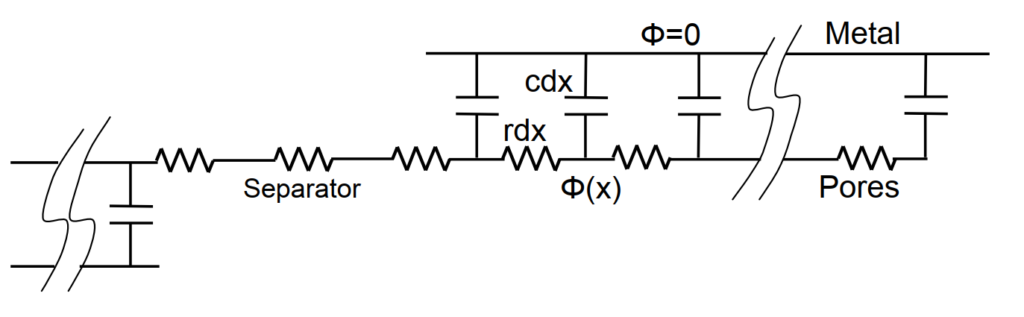
超級電容可模擬為RC傳輸線transmission line, 如圖5所示。假設兩厚度為L相同的多孔性電極對稱分佈，此時只看其中一個且0 < x < L. 這電解液充填的孔洞有一體積平均的電阻常數r與電容常數c. 忽略任何多孔性電極內或兩電極間空隙的電阻。孔洞間的平均電位能滿足下列線性擴散關係：

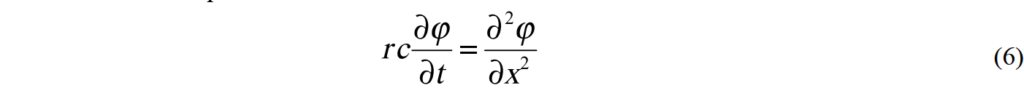
如果我們瞬間施加一電壓變化V於 t > 0 且 x = 0 , 電流的反應預測如下

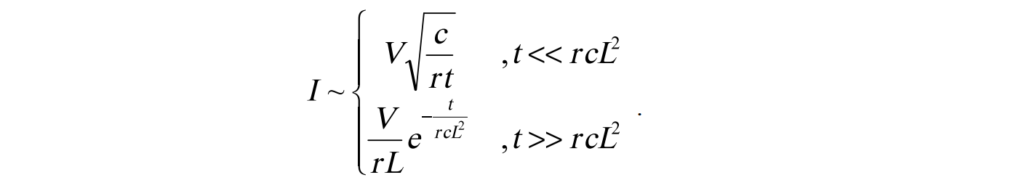
2. 一次電池

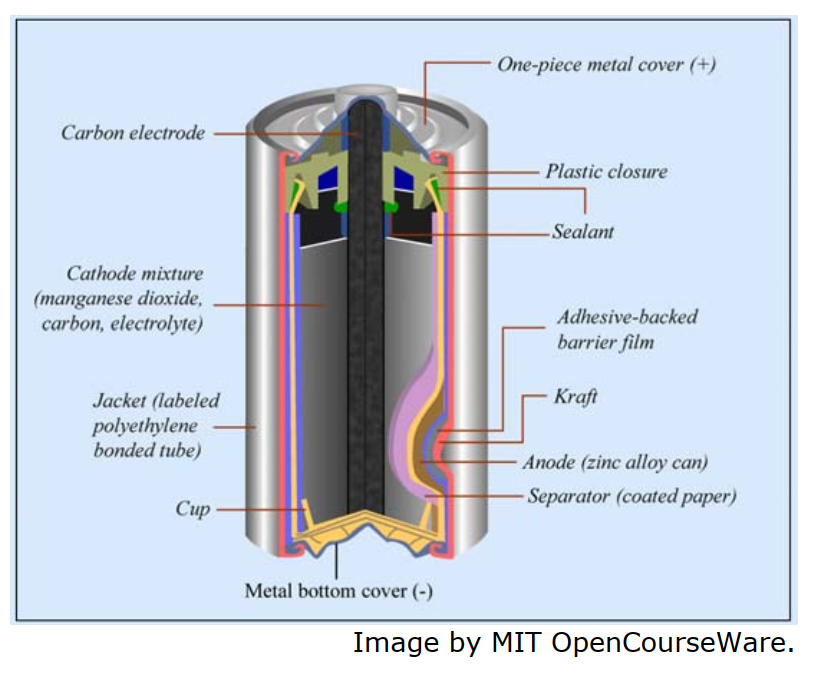
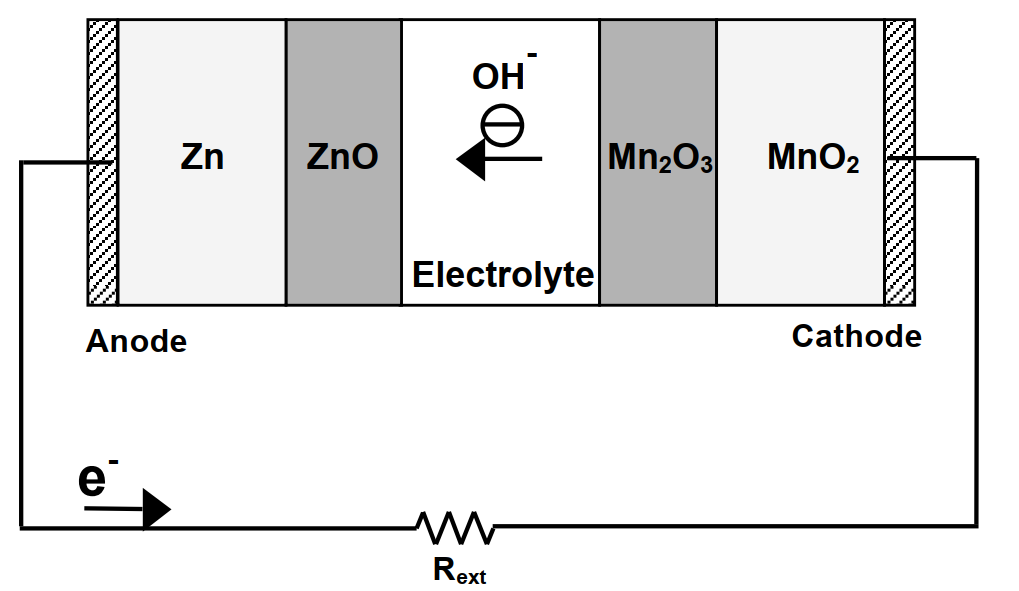
一次電池是指電池中的電化學反應是不可逆的；一次電池在組裝後可立即產生電流。一次電池無法充電因其化學反應是不可逆的且其反應材料無法回到初始狀態。勒克朗什Leclanche電池即為標準的一次電池。現代商業化的勒克朗什電池基本結構如圖6所示。詳細的反應為

陽極(氧化反應，產生電子)：

Zn + 2OH^– → ZnO + H₂O_(l) + 2e^–

陰極(還原反應，消耗電子)：

2MnO₂ + H₂O_(l) + 2e^– → Mn₂O₃ + 2OH^–

淨反應：

Zn + 2MnO₂ → Mn₂O₃ + ZnO

3. 二次電池

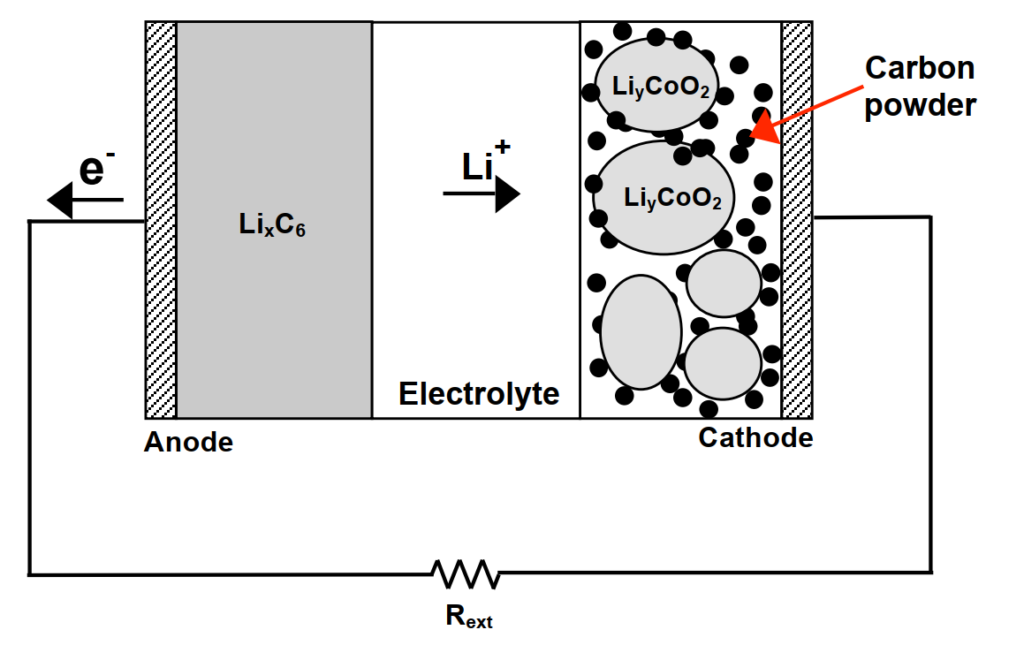
二次電池被稱為可充電電池因為他們的電化學反應是電可逆的。鋰離子電池如圖7是常見的二次電池範例。鋰離子在放電時由負極移往正極，而充電時相反。放電時負極為陽極並發生氧化反應，充電時負極則轉為陰極而發生還源反應。其放電的半反應為

陽極(氧化反應，產生電子)：

LiC₆ → Li⁺ + C₆ + e^–

陰極(還原反應，消耗電子)：

Li⁺ + e^– + CoO₂ → LiCoO₂

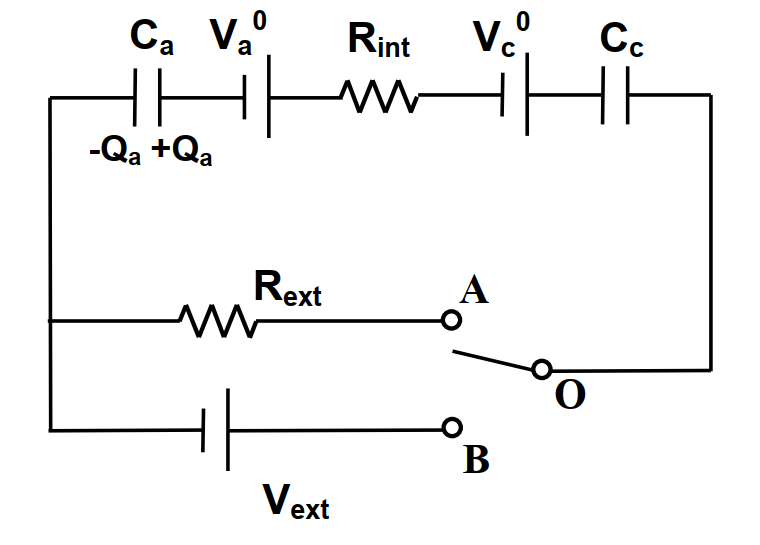
簡單二次電池的放電和充電可以模擬如圖8

1) 放電時(連結圖8的OA)

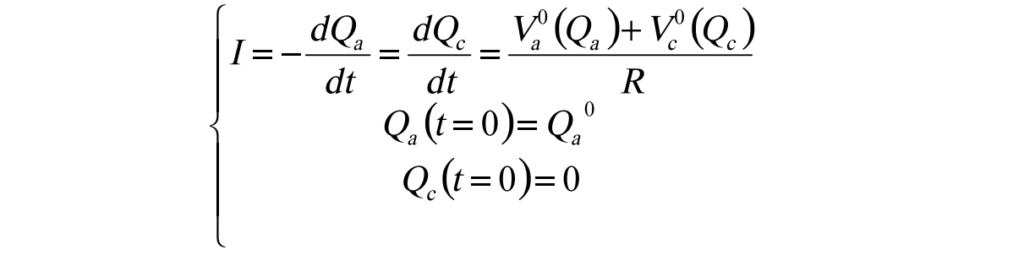
2)充電時(連結圖8的OB)

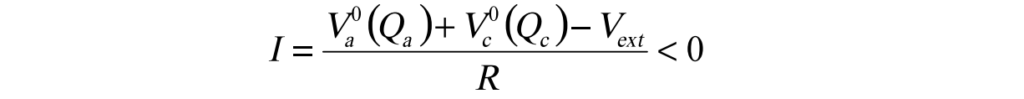
其中的R為總電阻R = R_int + R_ext

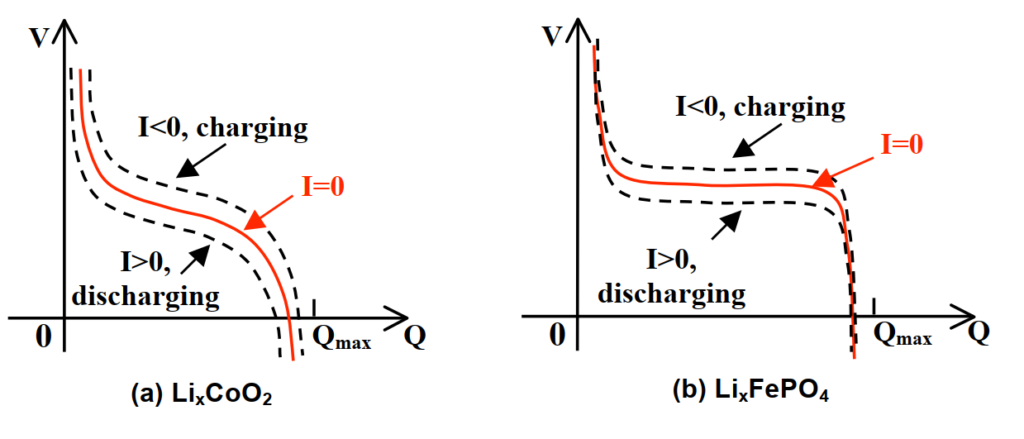
鋰離子電池的V與Q關係是高度非線性的，如圖9所示。細節會在課程9中討論。